А попытки решить задачу были? Хотелось бы их так же видеть.
Из содержательных соображений – в силу симметрии задачи должно отсутствовать движение вдоль плоскости. + должна сохраняться энергия и, вроде как, импульс.
Моё решение
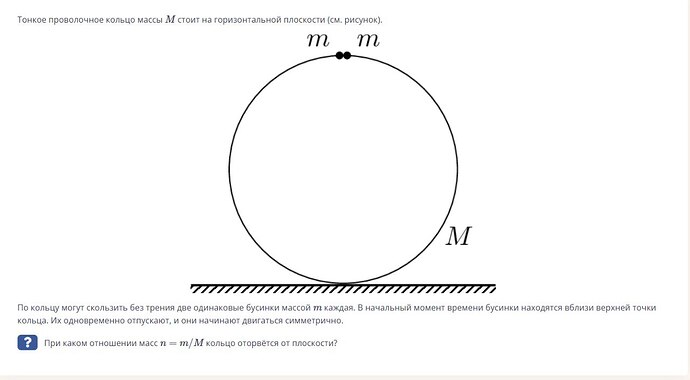
В силу симметрии достаточно рассмотреть одну из материальных точек.
Материальная точка действует на контур с помощью силы тяжести и центробежной силы. Первая равна mgcos(phi) и действует в сторону опоры контура. Вторая равна квадрату скорости точки деленной на радиус и естественно умнрденно на массу точки. Так как сил трения нет, сила давления контура на точку перпендикулярна контуру и следовательно не производит работы. Тогда можно вычислять скорость так как если бы точка свободно падала бы в поле силы тяжести. Далее вычисляя силу надо спроектировать ее на ось y с помощью косинуса или подобия треугольников. Спроектировав силу, мы видим что она зависит от положения точки, поэтому нам надо найти ее максимум с помощью обнуления производной. Ну и в итоге сделав все эти операции можно получить результат
Разбираемся с этим грязным контуром. Из-за симметрии нам достаточно приласкать только одну материальную точку – остальное доделаем по аналогии. Точка испытывает на себе две главные силы: силу тяжести (mgcos(φ), которая нежно прижимает её к контуру, и центробежную силу, которая разрывает её в разные стороны, словно кто-то не рассчитал свои движения. Вторая сила пропорциональна квадрату скорости и делится на радиус, умноженный на массу, короче, чем быстрее, тем сильнее разлетается.
Но, к счастью, силы трения здесь нет – контур гладкий, так что ничего её не держит. Сила давления строго перпендикулярна контуру и, как и некоторые бесполезные люди в жизни, вообще никакой работы не производит. Следовательно, скорость точки можно рассчитывать так, как если бы она просто падала в поле силы тяжести – просто и без лишних заморочек.
Теперь переходим к самой пикантной части: спроектируем силу на ось y, используя косинусы или подобие треугольников, чтобы правильно понять, насколько сильно точка прижимается. Видим, что сила зависит от её позиции – а это значит, что нужно найти её максимум, обнуляя производную (ну куда без этого, да?). Проделав все эти грязные манипуляции, наконец-то получаем окончательный результат.
Так что, ребята, главное — всё делать плавно, без лишней суеты и держать всё под контролем, иначе точка просто соскользнёт и улетит в бесконечность. ![]()